As observers in a 3-dimensional space, we cannot fully comprehend the idea of a 4-dimensional object. Here I will present one possible method of visualization — which, if nothing else, is something interesting to ponder. NOTE: This page is not about time as the fourth dimension. This is discussing a fourth spatial dimension.

To start, we shall apply this visualization in lower dimensions, then see a natural extension to higher dimensions. Firstly, consider a “2-dimensional function.” By this, I mean a function \(f:\mathbb{R}\to\mathbb{R}^2\) that can be visualized as a 2-dimensional plot on the Cartesian plane.

For this example, I chose the function \(f(x) = sin(x)\), as its behavior is something that is easily visualized (with prior knowledge of the sine function). The graph of \(sin(x)\) is pictured below:

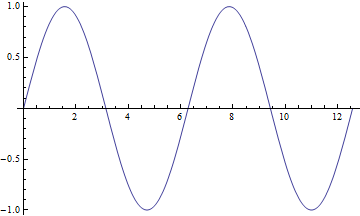
If we take \(sin(x)\) to be a function of time, then this graph models the value of \(sin(x)\) over time. This should be nothing new. Now, try to imagine the value of \(sin(x)\) at a single “slice” of time. For example, \(sin(0) = 0\). Since the value of \(sin(0)\) is just a one-dimensional point, we can place it on the real number line. If we merge all of the “slices” of \(sin(x)\) together, we should find ourselves looking at a graph identical to the one above. Again, this is nothing new. Now, observe the following animation. It is the value of \(sin(x)\) on the real number line, over time:

Note that all we’ve done is taken away a spatial dimension and added a timelike one. Through this, we can visualize \(sin(x)\) at any given moment, but not see its past values, or the values it will take in the future. Thus, we have a (limited) visualization of \(sin(x)\) in a single dimension.

Now that we’ve conquered the second dimension, let’s move on to the third one. For this, an easy visualization would be a function which describes the unit sphere in \(\mathbb{R}^3\). This corresponds to a 3-dimensional sphere in real life that has a radius of 1, which should be fairly easy to visualize. Just like we viewed \(sin(x)\) in the first dimension, we shall view this sphere in the second dimension. A “slice” of the function (let’s pretend it’s a function) will just be a 2-dimensional figure, instead of a 1-dimensional one. Here is the visualization:

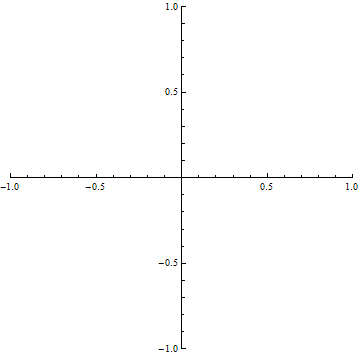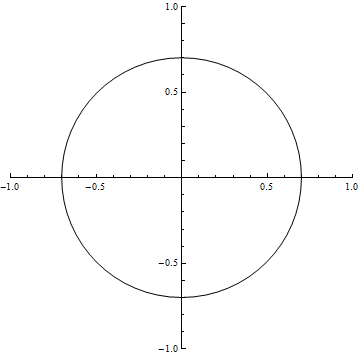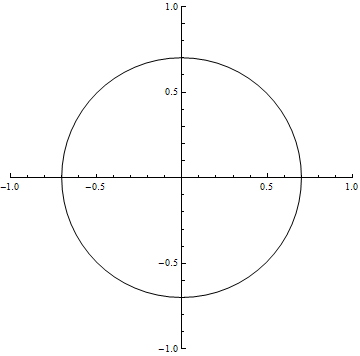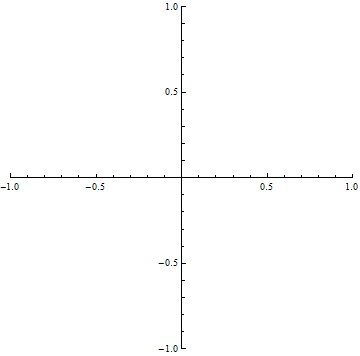
You’ll notice that at the edge of the sphere, the “slice” is a very very small circle. As time goes on, we get closer to the center of the sphere, and the radius of the corresponding slice increases until we hit the middle, where the radius is 1. The circles then decrease in radius as we travel away from the center of the sphere, until finally we reach its edge and there are no more “slices”. Note that ideally, the above animation should not repeat, as the function describing a sphere is not periodic! However, I decided to make it so in order to make sure you didn’t miss the animation. Since the 3rd dimension is easy to visualize, we can inspect this there to see what’s really going on:

Hopefully, it should be more clear now what is actually taking place. The surface of the plane that is going through the sphere is the last image! The circle in the last image represents where the sphere is intersecting with this plane as it travels through.

The final step is our transition to the 4-dimensional space. I chose to use a spherical example yet again, for simplicity. Don’t think too hard about what a 4-dimensional sphere (hypersphere) looks like, just think about its corresponding slices over time. It turns out that the slices of a hypersphere are our known and loved 3-dimensional spheres! Now, try to think of how a unit hypersphere would be represented. The hypersphere will actually be represented as a 3-dimensional sphere that, after popping into existence, grows to a radius of 1 and then shrinks back down, just like the corresponding result in the 3rd dimension! A visualization lies below:

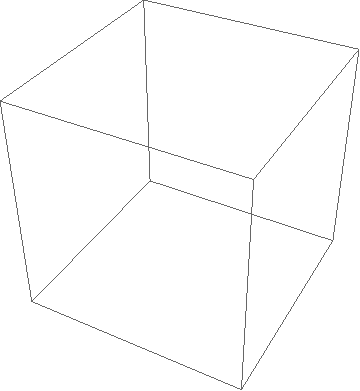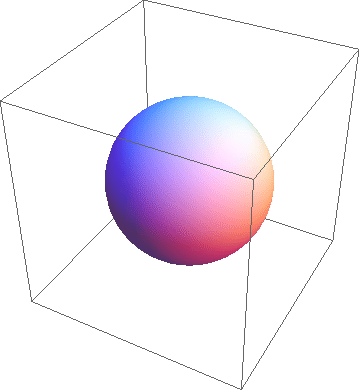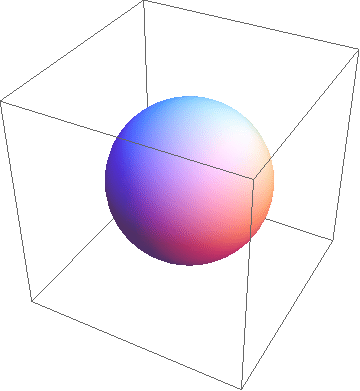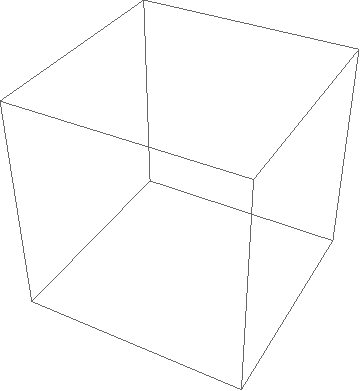
So hopefully by now, you understand what I mean by visualizing 4-dimensional objects. By removing a spatial dimension and adding a timelike one, we’ve been able to peek into the innards of geometric objects that don’t make a lot of sense intuitively.

Applying this argument, you could continue onto the 5th spatial dimension and beyond — however, slices composed of 4-dimensional objects do not sound very easy to visualize.